モーメントの公式
モーメントは以下の公式で求めることができます。
M:モーメント[Nm]
r :支点と力がかかっている位置までの距離[m]
M[Nm]= r[m] × F[N] F:かかっている[N]
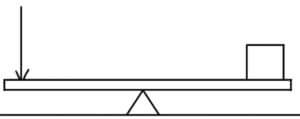
この公式を使って例題を解いてみましょう!
この釣り合っている力「F」を求めていきたいのですが、実はこれまでの知識だけではまだ解くことはできません。
足りない知識その1:力の公式
力にも次のような公式があります。
F:力[N]
m:質量(重さ)[kg]
F[N] = m[kg] × a[m/s2] a:加速度[m/s2]
加速度とは“トップスピードになるまでにどれぐらいのスピードで速くなっていくか”を表したものです。
重力の場合、“重力加速度[m/s2]”という名前に変わるのですが、意味は同じです。
問題に特に指定がない場合は“10[m/s2]”として計算すれば選択肢の答えと同じか、似たような数字になるはずです(9.8[m/s2]として計算する場合もあるので)。
足りない知識その2:モーメントの向き
風車のときに回転する方向を確認しましたよね?
これはモーメントを計算する上で重要なポイントになるのです!
モーメントを計算するときのルール(暗黙の了解)として、“反時計回りならプラス”、“時計回りならマイナス”で計算することになっています。

それでは一緒に解いていきましょう!

まずは『M[Nm] = r[m] × F[N]』を使ってみましょう!
M:モーメント[Nm]
r :支点と力がかかっている位置までの距離[m]
M[Nm]= r[m] × F[N] F:かかっている[N]
すると次の2つの式が出来上がります。
-
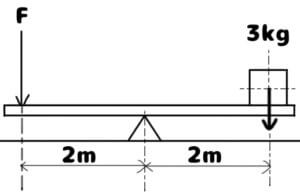
- M1[Nm] = 2[m] × F[N] ← 支点(△)より左のモーメント
- M2[Nm] = 2[m] × F?[N] ← 支点(△)より右のモーメント
このままでは右のモーメントの力(F?)が出せないですよね?
そこで『F[N] = m[kg] × a[m/s2]』が活躍します!!(重力加速度は10[m/s2]とします。)
F:力[N]
m:質量(重さ)[kg]
F[N] = m[kg] × a[m/s2] a:加速度[m/s2]
M2[Nm] = 2[m] × F?[N]
= 2[m] × (3[kg] × 10[m/s2])
= 2[m] × 30[N]
M2[Nm] = 60[Nm]
-
- M1[Nm] = 2[m] × F[N]
- M2[Nm] = 60[Nm]
ここで最後の知識です!
今回の問題では2つのモーメントは釣り合っています。
つまり2つのモーメントの大きさは同じなのです!
M1[Nm] = M2[Nm]
この式を変形(移行)すると
となります。
よって答えは
M1[Nm] – M2[Nm] = 0
(2[m] × F[N]) – 60[Nm] = 0
2F[Nm] = 60[Nm]
F[N] = 30[N] ← 答え!!


コメント